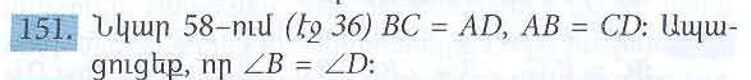
BC = AD

AB = CD

AC ընհանուր կողմ է

Ըստ III հայտանիշի եռանկյունները հավասար են։ Եթե կողմերը հավասար են հետևաբար անկյունները նույնպես հավասար են։

<B = <D

AB=CD

AD=BC

BE-ն ABC անկյան կիսորդն է

DF-ի ADC անկյան կիսորդն է

ա) Հայտնի է, որ AB=CD, AD=BC, իսկ AC-ն ընհանուր է:

Ըստ երրորդ հայտանիշի հասկացանք, որ ΔCDA=ΔCBA

Եթե կողմերը հավասար են հետևաբար անկյունները նույնպես հավասար են։

Եռանկյան կիսորդը անկյունը բաժանում է երկու հավասար անկյունների, հետևաբար <ABE=ADF

բ) AB=CD

Պարզել ենք, որ ΔCDA=ΔCBA

Հետևաբար` <A=<C, <B=<D

Ըստ III հայտանիշի կարող ենք ասել, որ ΔABE=ΔCDF

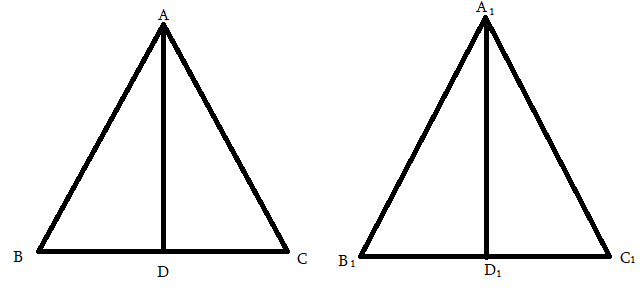
AB=A₁B₁

BD=B₁D₁

AD=A₁D₁

Ըստ եռանկյան երրորդ հայտանիշի կարող ենք ասել, որ եռանկյուն ΔABD = ΔA1B1D1

<A բաժանված է երկու հավասար անկյունների

<A=<A₁

<C₁=<C

AC=A₁C₁

Ըստ երկրորդ հայտանիշի կարող ենք ասել, որ ΔACD=ΔA₁C₁D₁

Եթե բոլոր եռանկյան կողմերը իրար հավասար են հետևաբար եռանկյունները հավասար են։