Առաջադրանքներ՝

1․Տրված է CAB եռանկյունը: Նշիր CA կողմին հանդիպակաց անկյունը:

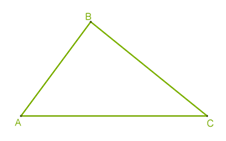
• CAB
• ACB
• ABC

2․CBA եռանկյան մեջ նշիր ABC անկյան հանդիպակաց կողմը:

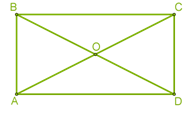
• BC
• AB
• DA
• BD
• DC
• AC

3․Ընտրիր գծագիրը, որում ցույց է տրված հավասարասրուն եռանկյուն: 

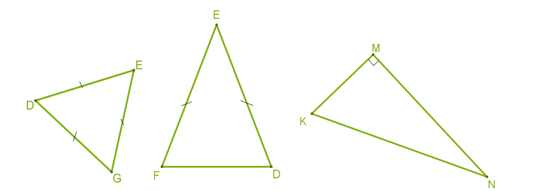
ΔFED

4․Ընտրիր ցուցադրված եռանկյան տեսակը: Հնարավոր է մի քանի ճիշտ պատասխան: 

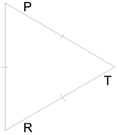
• ոչ հավասարասրուն
• հավասարակողմ
• բութանկյուն
• ուղղանկյուն
• հավասարասրուն
• սուրանկյուն

5․ Հաշվիր CBA եռանկյան պարագիծը, եթե AB=AC=CB=20 սմ:

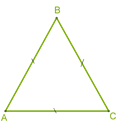
20+20+20=60սմ

P(CBA)= 60սմ

6․ Հաշվիր ABC եռանկյան պարագիծը, եթե CB=CA=600մմ և BA=800մմ:

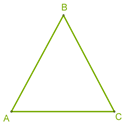
P(ABC)=600+600+800=2000մմ

7․Հաշվիր BCA եռանկյան պարագիծը, եթե CB=33մմ,BA=44մմ և CA=55մմ

 P(BCA)=33+44+55=132մմ

8․Որոշիր հավասարակողմ եռանկյան կողմը, եթե նրա պարագիծը հավասար է 111 սմ-ի:

111:3=37սմ

AB=BC=AC=37սմ

9․Հավասարասրուն եռանկյան պարագիծը հավասար է 154 դմ-ի, իսկ նրա սրունքը հավասար է 55 դմ-ի: Հաշվիր եռանկյան հիմքը:

55+55=110

154-110=44դմ

10․Եռանկյան պարագիծը հավասար է 1000 մմ-ի: Եռանկյան մի կողմը 400 մմ է: Հաշվիր եռանկյան մյուս երկու կողմերը, եթե հայտնի է, որ դրանք իրար հավասար են:

1000-400=600մմ

600:2=300մմ

11․Տրված է ΔCAB,BC=AC: Եռանկյան հիմքը 4 մ-ով փոքր է սրունքից:
CAB եռանկյան պարագիծը հավասար է 44 մ-ի: Հաշվիր եռանկյան կողմերը: 

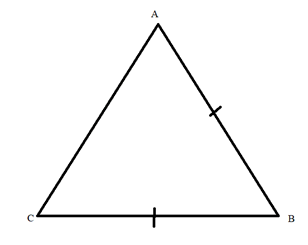
4+4=8մ

44-8=36մ

36:3=12մ

12+4=16մ

AB, CB=12մ

AC=16մ

12․ Տրված են KBP եռանկյան անկյունների մեծությունները՝ ∡K=65°, ∡B=85°, ∡P=30°: Թվարկիր եռանկյան կողմերը՝ ամենափոքրից մինչև ամենամեծը:

KB=65+85=150

BP=85+30=115

KP=65+30=95

KP<BP<KB

13․Տրված են երեք հատվածների երկարությունները: Որոշիր, թե արդյո՞ք դրանք կարող են լինել որևէ եռանկյան կողմեր:

ա). 2; 2; 2 

• այո
• ոչ

բ). 2; 5; 6 

• այո
• ոչ

գ). 5; 6; 45 

• ոչ
• այո

14․Տրված է՝ ΔABC,AC=CB:
Եռանկյան սրունքը 3 անգամ մեծ է հիմքից:
ABC եռանկյան պարագիծը հավասար է 280 սմ-ի: Հաշվիր եռանկյան կողմերը:

AB=CB=3AC

P=AB+AC+CB=280

280=AB+AC+CB=3AC+AC+3AC=7AC

AC=280:7=40

AB, BC=3AC=3*40=120

15․Հավասարասրուն եռանկյան պարագիծը 52 սմ է, իսկ մի կողմը՝ 10 սմ: Գտիր եռանկյան մյուս կողմերը:

10+10=20

52-20=32

AB=20

BC=20

AC=32