170․ Այն անհավասարումները, որոնք ունեն նույն լուծումը անվանում են համարժեք։

172․ ա) 5/x > 0
այն անհավասարմանը համարժեք է

5x > 0

5x = 0

x = 0

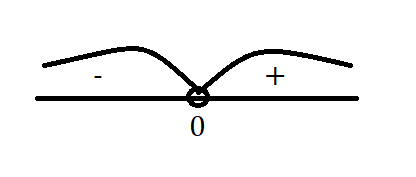
x∈ (0; +∞)

բ) -3/x < 0
այս անհավասարմանը համարժեք է

-3x < 0

-3x = 0

x = 0

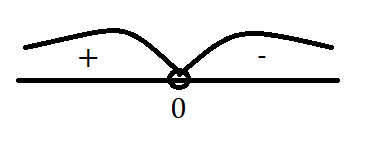
x∈ (0; +∞)

գ) 1/x-1 < 0
այս անհավասարմանը համարժեք է

1 (x-1) < 0

1 (x-1) = 0

x — 1 = 0

x = 1

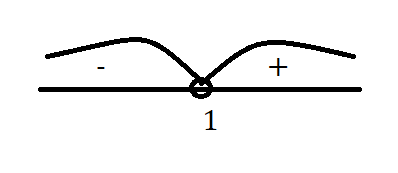
x∈ (-∞; 1)

դ) 1/2x+1 > 0
այս անհավասարմանը համարժեք է

2x + 1 > 0

2x + 1 = 0

2x = 1

x = 1/2

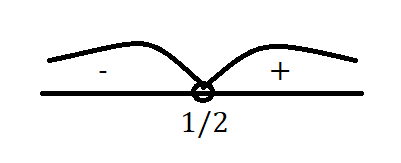
x∈ (1/2; +∞)

173. ա) x — 1/ x — 2 > 0

այս անհավասարմանը համարժեք է

(x — 1)(x — 2) > 0

(x — 1)(x — 2) = 0 = > [x — 1 = 0 = > [x = 1
[x — 2 = 0 [x = 2

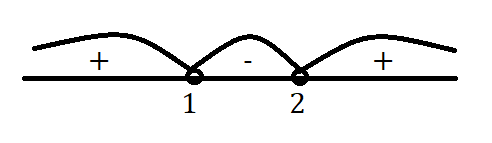
x∈ (-∞; 1) U (2; +∞)