1․Հավասարասրուն սեղանի անկյունագիծը կիսում է նրա բութ անկյունը: Սեղանի փոքր հիմքը 3 է, իսկ պարագիծը’ 42: Գտեք սեղանի մեծ հիմքը:

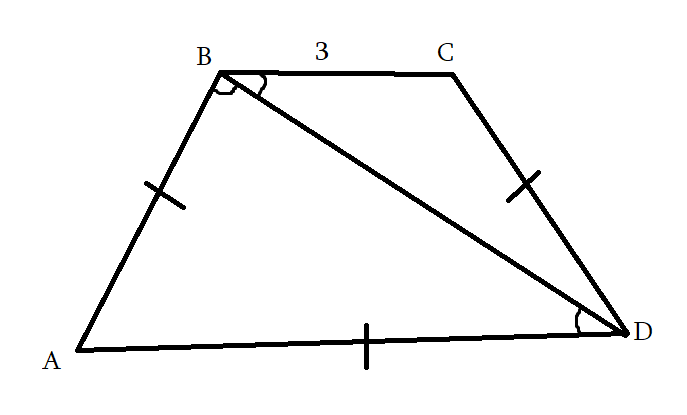
AB+CD+AD=42-3=39

AB=CD=AD=39/3=13

2․ C K-ն ABCD հավասարասրուն սեղանի AD մեծ հիմքին տարած բարձրությունն է: Գտեք KD-ն, եթե ВС=9, AD=15:

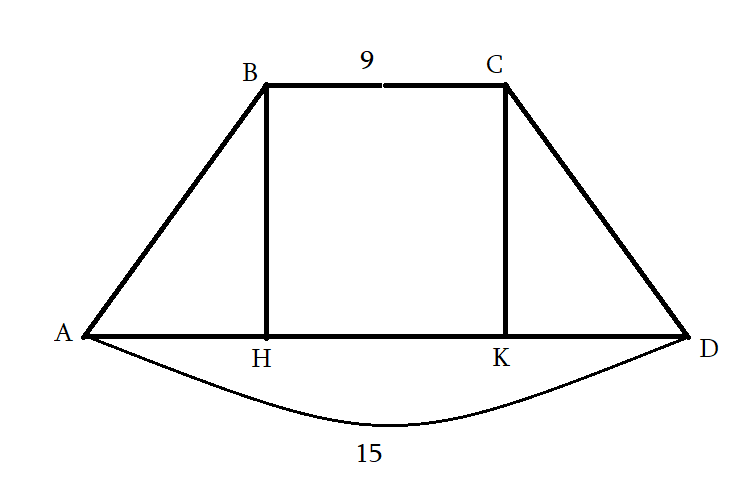
AH+KD=15-9=6

KD=6:2=3

3․ CK-ն ABCD հավասարասրուն սեղանի AD մեծ հիմքին տարած բարձրությունն է: Գտեք սեղանի հիմքերը, եթե նրանց գումարը 18 է, իսկ KD-ն 1 է:

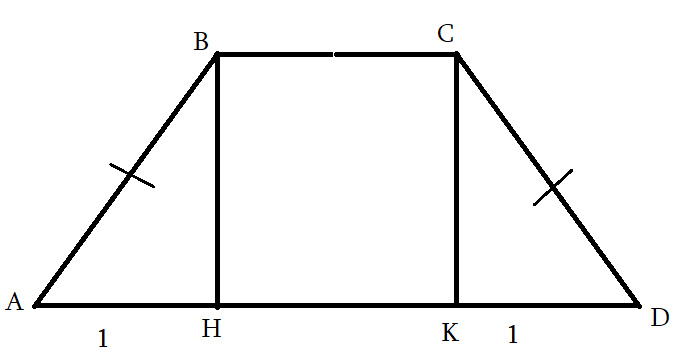
BC+AD=18

KD=AH=1

AH+KD=1+1=2

HK=BC=(18-2):2=8

AD=8+2=10

4․CK-ն ABCD հավասարասրուն սեղանի մեծ հիմքին’ AD-ին տարած բարձրությունն է: Գտեք АК-ն, եթե BC=7, AD= 16:

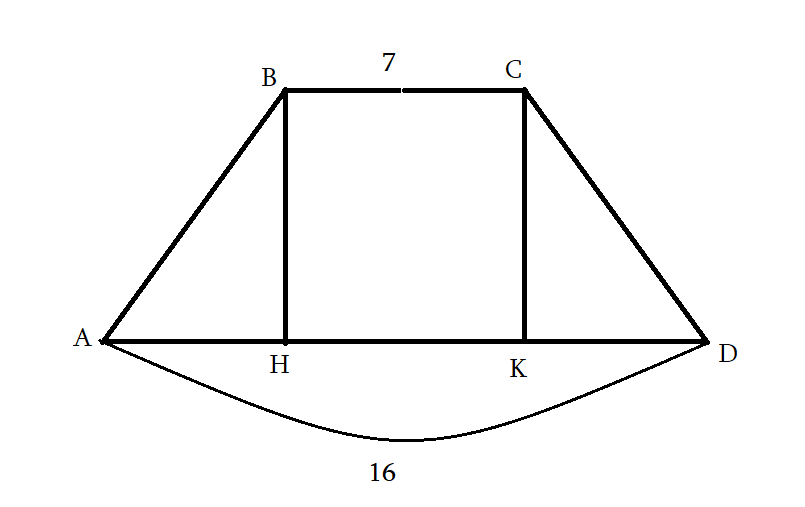
BC=HK=7

(AH+KD)-HK=16-7=9

AH=KD=9:2=4,5

AK=4,5+7=11,5

5․Գտեք ուղղանկյուն եռանկյան ներքնաձիգին տարած միջնագիծը, եթե
ներքնաձիգը 16 է:

Ըստ հայտանիշի ուղղանկյուն եռանկյան գագաթից տարված միջնագիծը հավասար է ներքնաձիգի կեսին:

AD=BC:2=16:2=8

6․ABCD շեղանկյան անկյունագծերը հատվում են О կետում, անկյուն АВС=60°: Գտեք АОВ եռանկյան անկյունները:

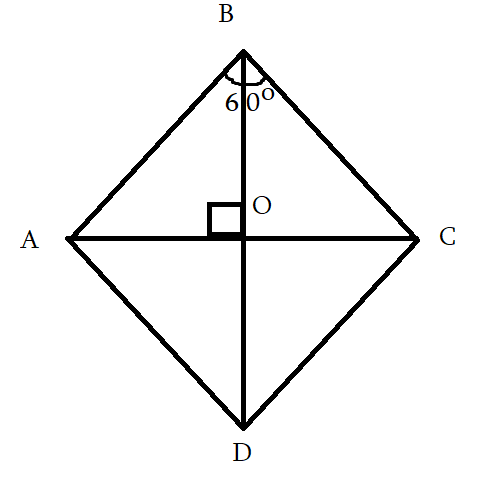
<ABO=60:2=30^o

<AOB=90^o

<BAO=180-(90+30)=60^o

7․ABCD շեղանկյան անկյունագծերը հատվում են О կետում, ընղ որում АО=3,6, անկյուն ABC=60°: Գտեք շեղանկյան կողմը:

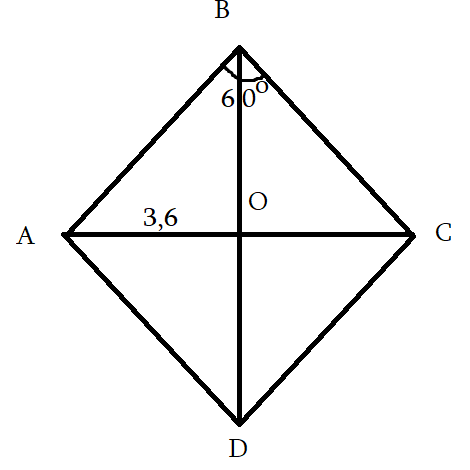
AO=OC=3,6

AC=3,6*2=7,2

<ABC=60^o

<ABC=<ADC=60^o

∆ABC և ∆ADC հավասարասրուն են և ինչպես գիտենք, հիմքին առընթեր անկյունները հավասար են:

<BAO=<BCO=(180-60):2=60^o

Եռանկյունը հավասարասրուն է

AC=AB=BC=CD=AD=7,2

8․ ABCD շեղանկյան A անկյունը 130° է: Գտեք ABC եռանկյան անկյունները:

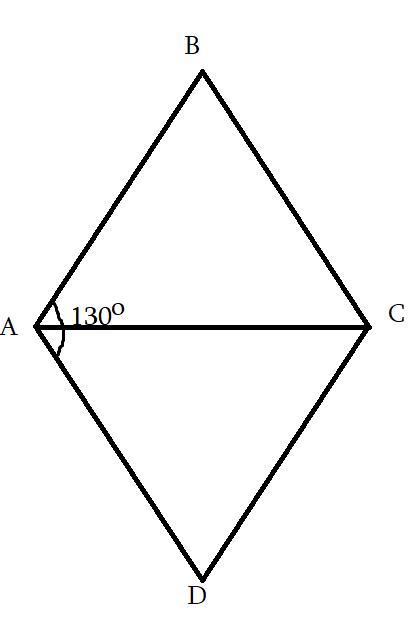
<BAC=130:2=65^o

∆ABC հավասարասրուն է, ուրեմն

<BCA=<BAC=65^o

<ABC=180-(65+65)=50^o