Առաջադրանքներ
1․Որքա՞ն է ներգծյալ անկյունը, որը հենված է 230° աստիճանային չափով աղեղի վրա:
230o : 2 = 115o
2․Որքա՞ն է կենտրոնային անկյունը, եթե նրան համապատասխանող ներգծյալ անկյունը 38° է:
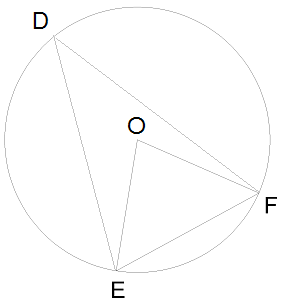
∪EF = 2 * <D = 2 * 38o = 76o
<EOF = ∪EF = 76o
3․Դիցուք CAB անկյունը 11° է:
Որքա՞ն է CnB աղեղի աստիճանային չափը՝
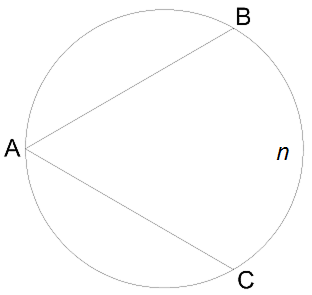
4․
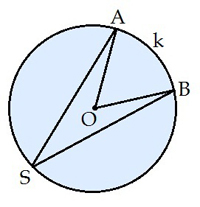
Գտիր ASB անկյունը, եթե ASB աղեղի աստիճանային չափը 205° է:
∪AkB = 360 — 205 = 155o
<ASB = ∪AkB : 2 = 155 : 2 = 77,5o
5․
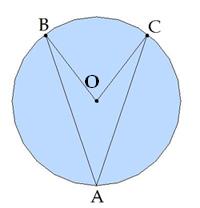
∪AB=110°, ∪AC=99°
Գտիր BOC և BAC անկյունները:
∪BAC = ∪BA + ∪AC = 110 + 99 = 209o
∪BC = 360 — 209 = 151o
<BOC = ∪BC = 151o
<BAC = ∪BC : 2 = 151 : 2 = 75,5o
6․
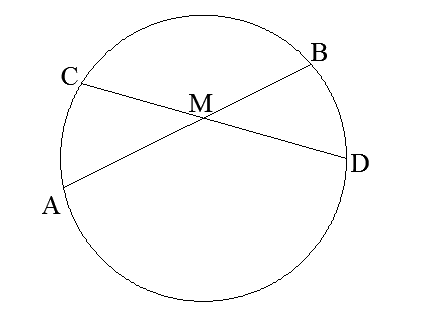
Հաշվիր DC լարի երկարությունը, եթե՝
AM =1մմ
MB =6մմ
CM=2մմ
AM * MB = CM * DM = 1 * 6 = 2 * DM
6 = 2MD
DM = 6/2 = 3մմ
DC = DM + CM = 3 + 2 = 5մմ
7․Հաշվիր AOB եռանկյան անկյունները, եթե ∪AnB=122°
……………………………….n
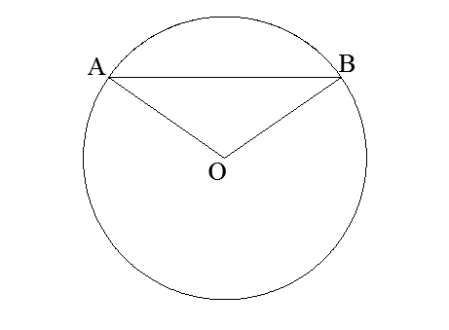
<AOB = ∪AnB = 122o
<OAB = <OBA = (180 — 122) : 2 = 58 : 2 = 29o
