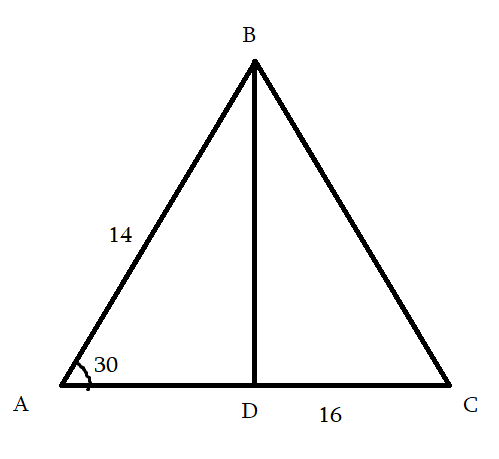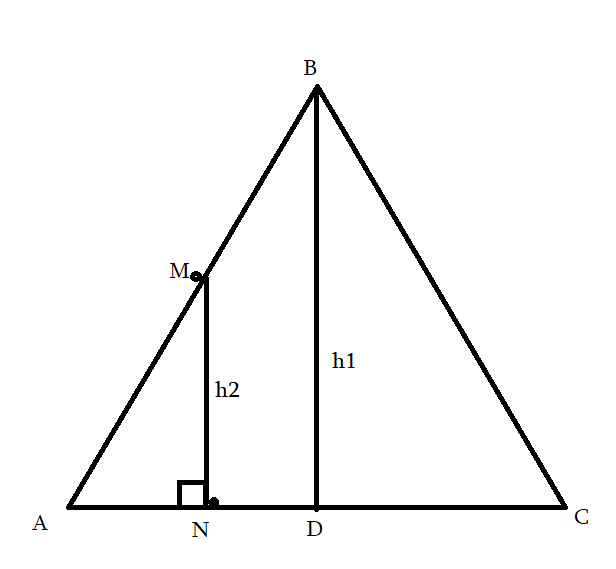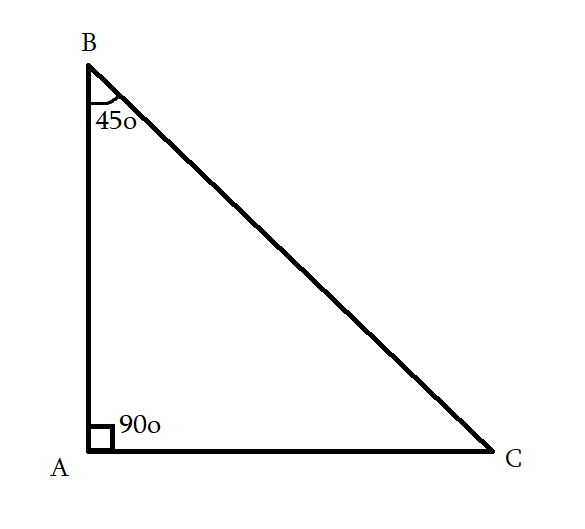345-350

ա)

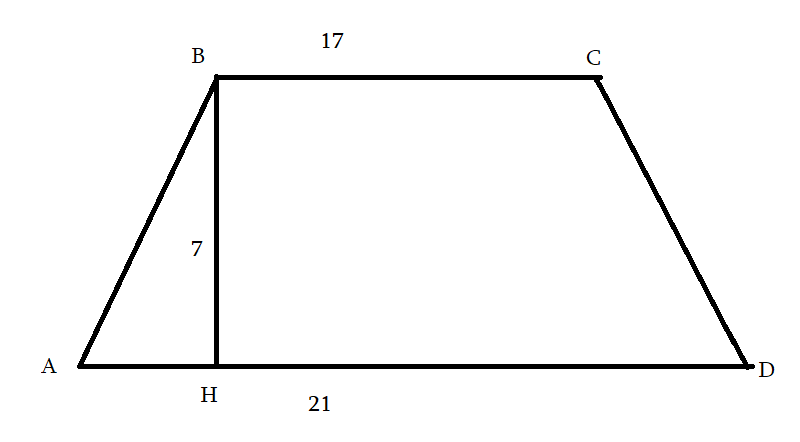
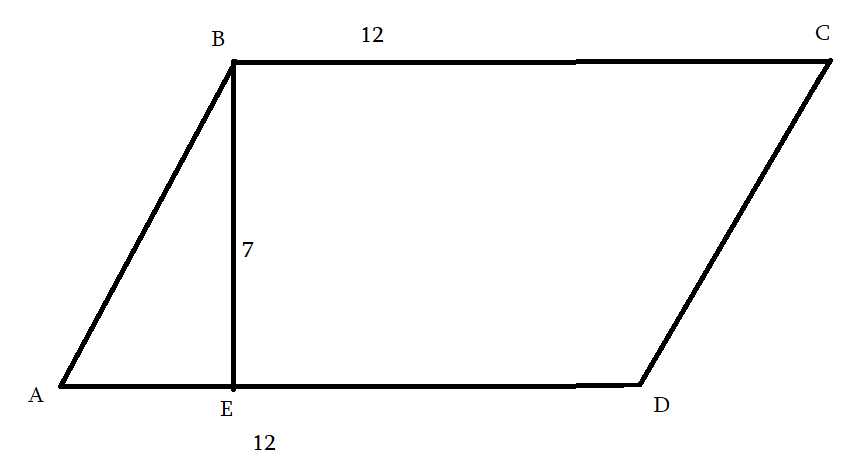
AD = 21

BC = 17

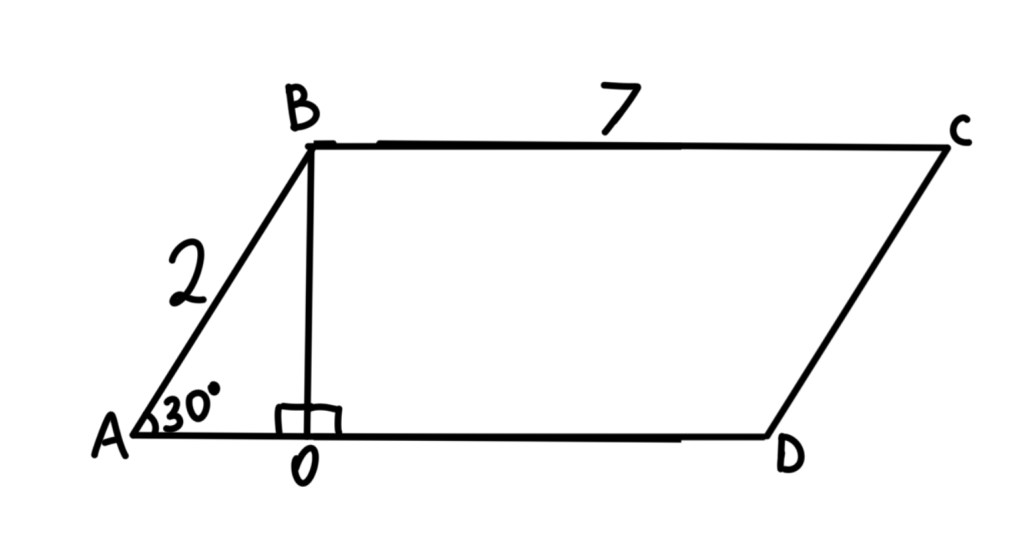
BH = 7

S_ABCD = 7*(17+21)/2 = 133

բ)

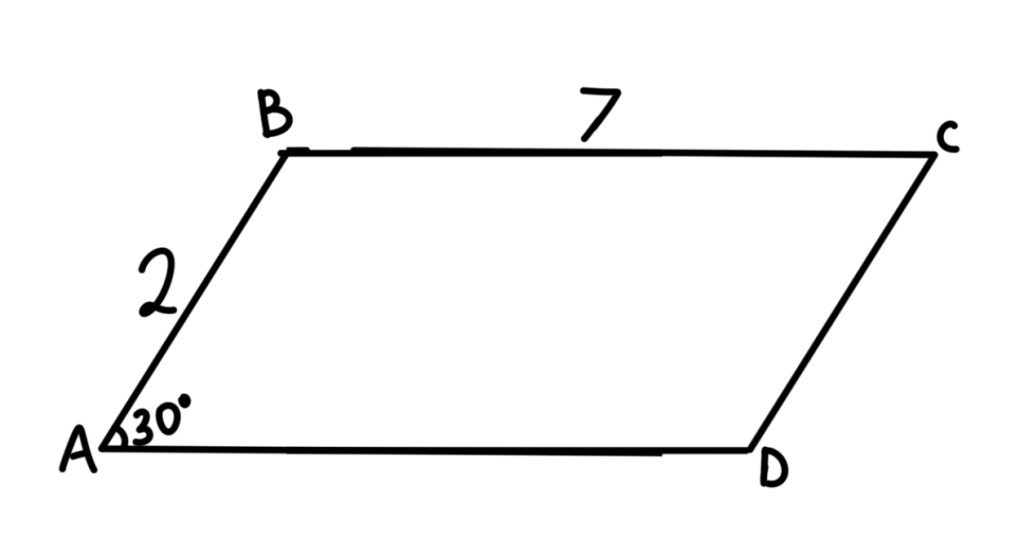
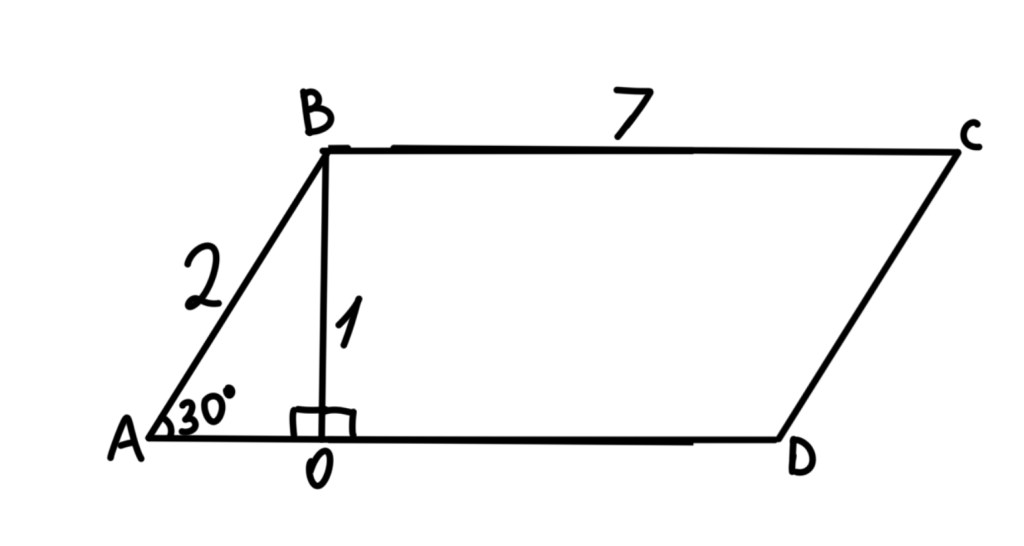
<D = 30o

AD = 10

BC = 2

CD = 8

Ըստ ուղղանկյուն եռանկյան հայտանիշի 30o-ի դիմաց ընկած կողմը հավասար է ներքնաձիգի կեսին, ուրեմն՝

CH = CD/2 = 8/2 = 4

SABCD = 4*(2+10)/2 = 24

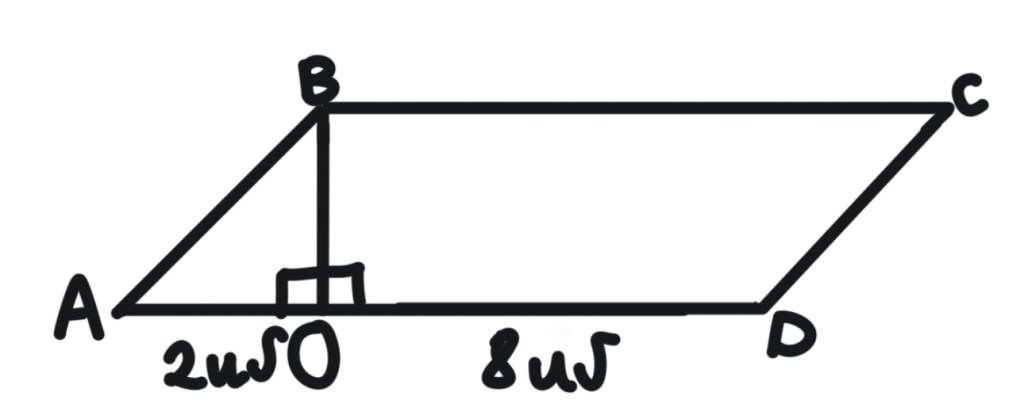
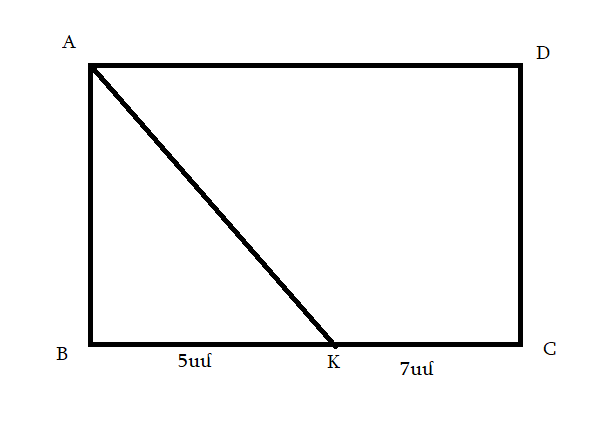
գ)

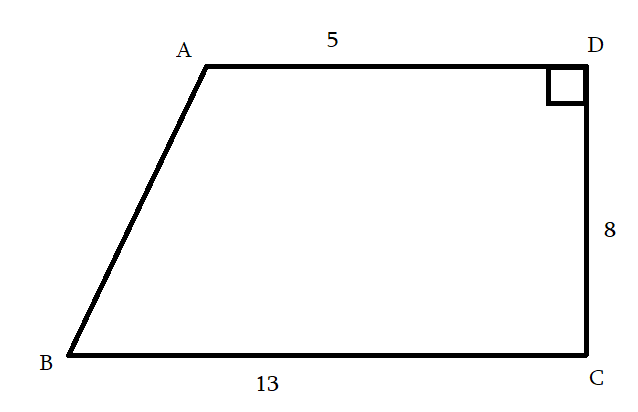
AD = 5

CD = 8

BC = 13

S_ABCD = 8*(5+13) = 72

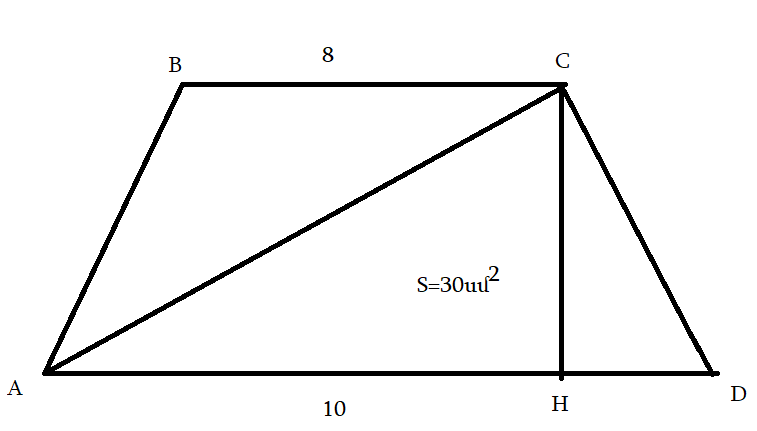
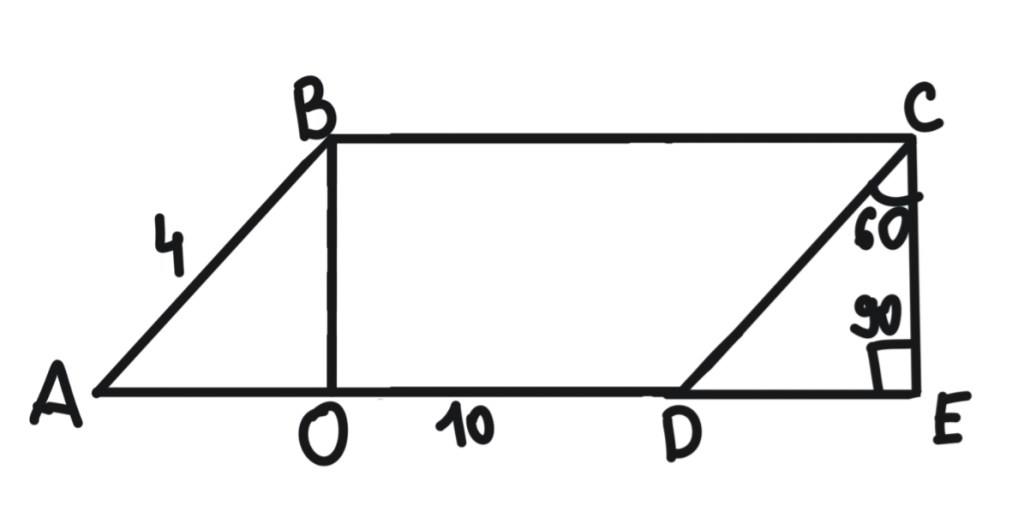
CH = 30:10*2=6

S_ABCD = 6*(10+8)/2 = 54

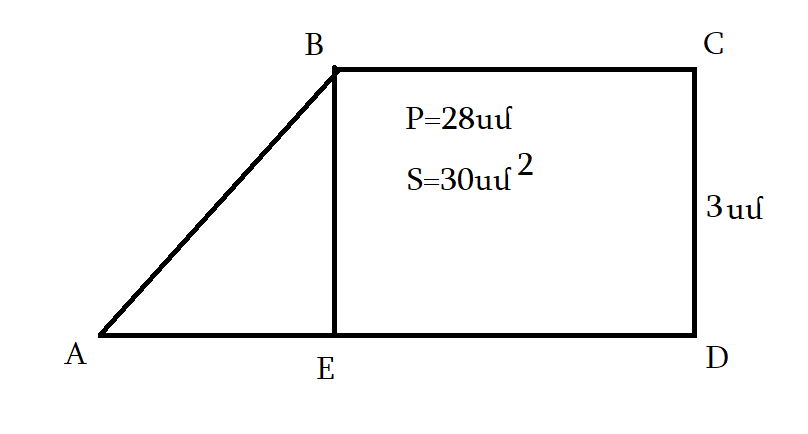
S_ABCD = 30սմ²

P_ABCD = 28սմ

AB = ?

SABCD = (AD + BC) * CD/2 = 30սմ2

AD + BC = 2*SABCD/CD = 2 * 20/3 = 20

PABCD = AB + BC + CD + AD

AB = PABCD — BC + CD + AD

AB = 28 — 20 — 3 = 5սմ

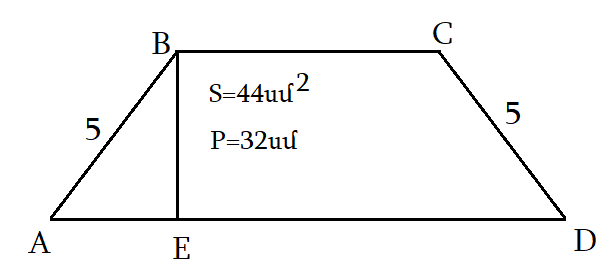
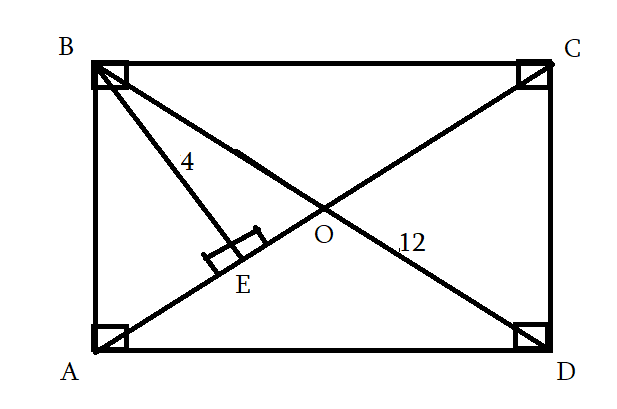
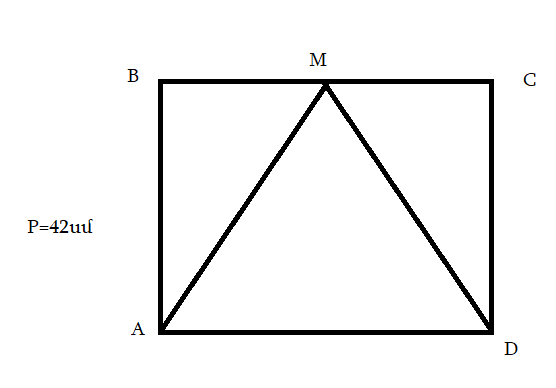
PABCD = 32sm

SABCD = 44sm2

AB = CD = 5

PABCD = AB + BC + CD + AD

PABCD = 2AB + BC + AD

32 = 25 + (BC + AD)

BC + AD = 32 — 10 = 22

2SABCD = (AD + BC) * BE

BE = 2SABCD / (AD + BC)

BE = 2 * 44 / 22 = 88/22 = 4

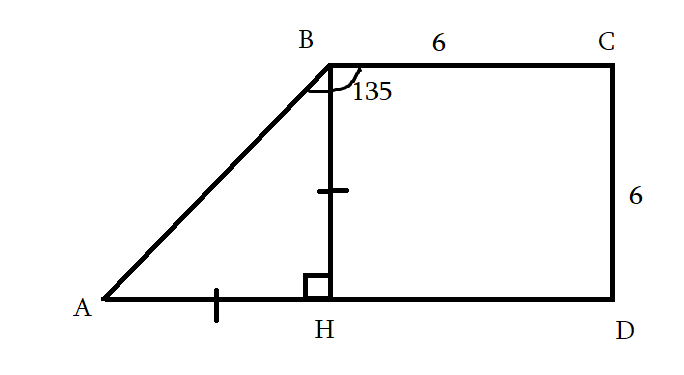
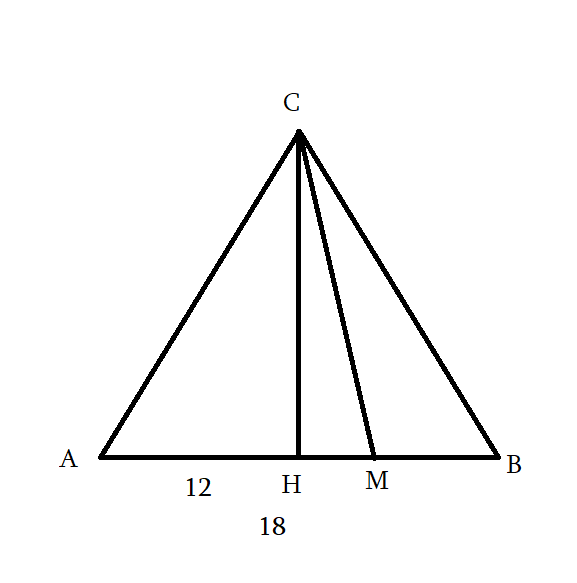
BC = CD = 6

S — ?

<A = 45o

S = BC+AD/2 * CD

AH = HB = CD = 6

HD = BC 6

S = 6+12/2 * 6 = 54սմ²

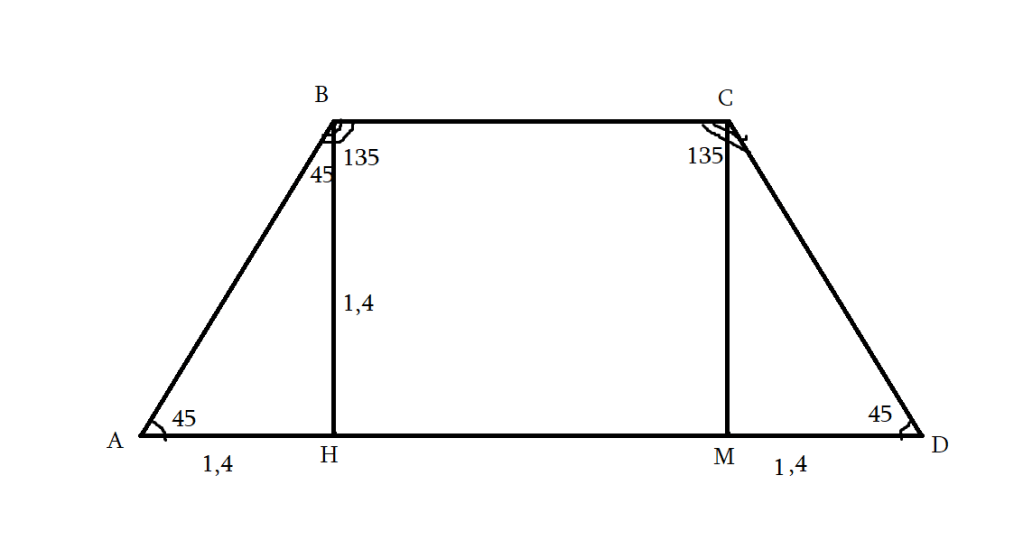
AB = CD

<B = <C = 135o

AH = 1,4

HD = 3,4

S — ?

AD = 4,8

BH = 1,4

BC = HM = 2

S = 4,8 + 2 / 2 * 1,4 = 68/10 * 7/10 = 476/100 = 4,76

1․Զուգահեռագծի կողմերից մեկը 12 է, նրան տարած բարձրությունը’ 7: Գտեք գուգահեռագծի մակերեսը։

S = 12*7 = 84

2․Զուգահեռագծի մակերեսը 63 է, կողմերից մեկը’ 9: Գտեք այդ կողմին տարված բարձրությունը:

63 : 9 = 7

3․Զուգահեռագծի կիկ կողմերը 6 և 10 են: Փոքր կողմին տարած բարձրությունը 9 է: Գտեք մեծ կողմին տարած բարձրությունը:

AB = CD = 6

BC = AD = 10

S = 6*9 = 54

BM = 54:10 = 5,4

4․Զուգահեռագծի կից կողմերը 8 և 11 են, իսկ սուր անկյունը’ 30°: Գտեք զուգահեռագծի մակերեսը:

AB = CD = 8

BC = AD = 11

<A = <C = 30o

<BMA = 90o

<ABM = 180 — (90+30) = 60o

Ըստ ուղղանկյուն եռանկյան հայտանիշի 30o-ի դիմաց ընկած կողմը հավասար է ներքնաձիգի կեսին, ուրեմն՝

BM = AB/2 = 8/2 = 4

S = 4*11 = 44

5․Եռանկյան կողմերից մեկը 11 է, նրան տարած բարձրությունը’ 7: Գտեք եռանկյան մակերեսը:

11*7/2 = 38,5

6․Եռանկյան մակերեսը 108 է, կողմերից մեկը’ 27: Գտեք այղ կողմին տարած բարձրությունը:

108=27*h

h = 108 : 27 = 4

7․АВС եռանկյան մեջ <A=30°, АВ=14, АС=16: Գտեք եռանկյան մակերեսը:

<A=30°

АВ=14

АС=16

Ըստ ուղղանկյուն եռանկյան հայտանիշի 30o-ի դիմաց ընկած կողմը հավասար է ներքնաձիգի կեսին, ուրեմն՝

BD = AB/2 = 14/2 = 7

S = 7*16/2 = 56

8․Ուղղանկյուն եռանկյան էջերը 7 և 12 են: Գտեք եռանկյան մակերեսը:

AB = 7

AC = 12

S = 7*12/2 = 42

337,339,340

ABC=?

BD=AC=12

S=AC*BE/2=12*4/2=24սմ²

AB=18

AM=12

S_AMB : S_AMC = ?

S_ABC=AB*h=18*h

S_AMC=AM*h = 12*h

S_ABC:S_AMC = 18h:12h = (6*3):(6*2) = 3/2

AB = 2AM

AC = 3AN

S_ABC : S_AMN = ?

h₁ = 2h₂

S_ABC = AC * h₁ = 3AN * h₁ = 3AN * 2h₂ = 6ANh₂

SAMN = AN * h2 = ANh₂

S_ABC : S_AMN = 6ANh₂ : ANh₂ = 6 : 1

Խնդիրներ՝ 329 – 333

ա) S = 7*11/2 = 38,5սմ

բ) h = 37,8/1 = 14*h/2 = 75,6սմ

գ) a = 2² = 4սմ

AN=?

S = AB*CH/2 = 16*11/2 = 88

88/1 = 22*AN/2

AN = 88*2/22=8սմ

AB=7,5

BC=3,2

CH=2,4

AN = ?

S = AB*CH/2 = 7,5*2,4/2=9

91=3,2*AN/2

AN=9*2/3,2=5,625

ա) S = AC*AB/2=11*4/2=22սմ²

բ) 3dm=30sm

S=AC*AB/2=30*12/2=180sm2=1,8dm2

<A=90^o

<B=45^o

<C=180-(90+45)=45^o

Եթե երկու առընթեր անկյունները հավասար են, ապա եռանկյունը հավասարասրուն է:

AB=AC

S=AB*AC/2=14*14/2=98սմ²

1․Քաառակու կողմը 7 է: Գտեք նրա մակերեսը:

S=7*7=49

2․քառակուսու մակերեսը 81 է: Գտեք նրա կողմը:

S = 80:9=9

3․Քառակուսու մակերեսը 121 է: Գտեք նրա պարագիծը:

121:11=11

P =11+11+11+11=44

4․Ուղղանկյան կից կողմերը 15 և 6 են: Գտեք ուղղանկյան մակերեսը:

S=15*6=90

5․Ուղղանկյան կողմերից մեկը 13 է, մյուսը 3 անգամ մեծ է նրանից: Գտեք ուղղանկյան մակերեսը։

13*3=39

S =13*39=507

6․Ուղղանկյան կողմերից մեկը 4-ով մեծ է մյուսից, իսկ մակերեսը 96 է: Գտեք ուղղանկյան կողմերը։

S=x*y=96

y=x+4

x*(x+4)=96

x=8

8*(8+4)=96

7․Ուղղանկյան կողմերից մեկը 5 անգամ փոքր է մյուսից, իսկ մակերեսը 125 է: Գտեք ուղղանկյան կողմերը:

S=x*y=125

y=x:5

x*(x:5)=125

x=25

25*(25:5)=125

8․Զուգահեռագծի կողմերից մեկը 12 է, նրան տարած բարձրությունը՝ 7: Գտեք գուգահեռագծի մակերեսը:

S=12*7=84

9․Զուգահեռագծի մակերեսը 63 է, կողմերից մեկը՝ 9: Գտեք այդ կողմին տարված բարձրությունը;

63:9=7

10․Զուգահեռագծի կից կողմերը 6 և 10 են: Փոքր կողմին տարած բարձրությունը 9 է: Գտեք մեծ կողմին տարած բարձրությունը։

11․Զուգահեռագծի կից կողմերը 8 և 11 են, իսկ սուր անկյունը’ 30°: Գտեք զուգահեռագծի մակերեսը:

12․Զուգահեռագծի կողմերից մեկը 7 է, իսկ 18 երկարությամբ անկյունագիծը նրա հետ կազմում է 30°-ի անկյուն: Գտեք զուգահեռագծի մակերեսը:

<B=180-30=150⁰

Պատ.՝ 1:

P=2+2+7+7=18սմ

Պատ.՝ 4:

30⁰-ի դիմաց ընկած կողմը հավար է ներքնաձիգի կեսին, ուրեմն՝

BO=2÷2=1

Պատ.՝ 1:

S=1×7=7սմ²

Տանը՝ 322, 323, 325,

S=20սմ²

S=AD×h

AD=2+8=10սմ

20=10×h

h=20÷10=2սմ

AO=OB=2սմ

<AOB=90⁰

<A+<ABO=180-90=90

Քանի որ եռանկյուն AOB-ն հավասարասրուն է, ուրեմն՝

<A=<ABO=90÷2=45⁰

<A=<C=45⁰

<B=45+90=135⁰

<B=<D=135⁰

S=?

<DCE=60⁰

<BCD=90-60=30⁰

<A=<BCD=30⁰

30⁰-ի դիմաց գտնվող կողմը հավասար է ներքնաձիգի կեսին, ուրեմն՝

BO=4÷2=2սմ

S=10×2=20սմ²

AD-CD=10

P=?

AD=10+CD

S=AD×BH

S=CD×BM

S=(10+CD)×3x

S=CD×5x

1=3×(10+CD)

1=5×CD

5CD=3(CD+10)

5CD=3CD+30

2CD=30

CD=15

CD=AB=15

AD=10+CD=10+15=25

AD=BC=25

P=15+15+25+25=80

314ա,դ, 315, 316, 320

ա)

S=a*h=12*15=180սմ²

դ)

a=21a/ 1/2a=21/ 1/2=10,5

S=12*13=156սմ²

90^o-ի դիմաց գտնվող կողմը հավասար է ներքնաձիգի կեսին:

BH=12:2=6սմ

S=6*13=78սմ²

△BNC-ն ուղղանկյուն եռանկյուն է

30^o-ի դիմաց գտնվող կողմը հավար է ներքնաձիգի կեսին, ուրեմն՝

BC=BN*2=3*2=6սմ

S=BM*BC=2*6=12սմ²

Առաջադրանքներ՝ 307 – 312

P=32սմ

32:4=8սմ

S=8*8=64սմ²

64:45=1,4սմ

△ABM-ը ուղղանկյուն եռանկյուն է

30^o աստիճանի դիմացի կողմը հավասար է ներքնաձիգի կեսին, ուրեմն՝

AB=BM:2=20:2=10սմ

S=10*10=100սմ²

<BAK=45^o

<B=90^o

<BKA=180-90-45=45^o

AB=BK=5սմ

BC=BK+KC=5+7=12սմ

BC=AD=12սմ

S=12*5=60սմ²

P=42սմ

<BAM=<MAB=<CDA=<MDC=45⁰

<B=90^o

<BMA=180-90-45=45^o

AB=a

BC=2a

P=(a+2a)*2=6a=42սմ

a=42/6=7

2a=14

S=14*7=98սմ²

S₁=5,5*6=33մ²

30սմ=0,3մ

5սմ=0,05մ

S₂=0,3*0,05=0,015մ²

33/0,015=2200 (մանրատախտակ)

S₁=3*2,7=8,1մ²

15սմ=0,15մ

S₂=0,15*0,15=0.0225մ²

8,1/0,0225=360 (սալիկ)

Դասագրքից՝ 298, 299, 301, 303, 305, 306

ա) S=1,2*1,2=1,44սմ²

բ) S=3,4*3,4=9,6դմ²

գ) S=3 1/3*3 1/3=100/9մ²

ա) 16սմ²=4սմ*4սմ

բ) 25դմ²=5դմ*5դմ

գ) 2,25մ²=1,5մ*1,5մ

ա) Քառակուսին կմեծանա 9 անգամ

բ) Քառակուսին կփոքրանա 4 անգամ

ա) S=8,5*3,2=27,2սմ²

բ) S=2/3*1,2=0,8սմ²

գ) b=684:32=21,375սմ

դ) b=4,5դմ=45սմ

a=1215:45=27սմ

P=4x+4x+3x+3x=14x=28սմ

x=28/14=2սմ

4x=4*2=8սմ

3x=3*2=6սմ

a=12սմ

S=96սմ²

b=96:12=8սմ

P=12+12+8+8=40սմ